一、什么是PCP平价公式?
Put-CallParity(简称PCP)平价公式是经典的期权定价模型之一。因其限制条件较少和公式简洁等因素,该模型在场内外期权市场得以广泛运用。PCP平价公式表述的是相同行权价格、相同到期日的欧式无分红期权的认购期权(C)、认沽期权(P)、标的证券价格(S)和行权价格(K)之间的关系。其具体公式如下:
C+Ke-r(T-t)=P+S
公式中K为认购和认沽期权合约的行权价格,Ke-r(T-t)表示对金额K折现,r为无风险利率,T-t为期权合约剩余期限
二、公式如何推导?
对于公式的推导,我们通常使用资产复制的形式。我们看以下两种资产组合
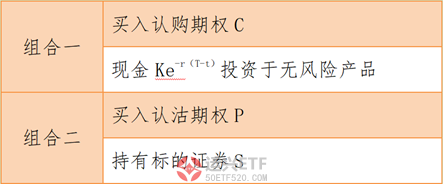
到期后,标的证券S会出现两种情况。
第一种情况,如果到期标的证券S的价格大于K元,我们观察两种组合的状态:
组合一中的认购期权C,由于标的价格大于行权价格,所以投资者选择行权,即用K元购买标的证券S;而持有的Ke-r(T-t)元投资于无风险产品,到期正好获得K元的回报,用于行权,所以最终投资者只持有标的证券S。
组合二中的认沽期权P,由于标的价格大于行权价格,所以投资者放弃权利,即不行权,合约价值归零;而持有的标的证券S没有任何变化,所以最终投资者只持有标的证券S。
因此,当到期标的证券价格S大于K元时,组合一等于组合二,都是持有标的证券S。
第二种情况,如果到期标的证券S的价格小于K元,我们观察两种组合的状态:
组合一中的认购期权C,由于标的价格小于行权价格,所以投资者放弃权利,即不行权,合约价值归零;而持有的Ke-r(T-t)元投资于无风险产品,到期正好获得K元的回报,所以投资者最终持有K元现金。
组合二中的认沽期权P,由于标的价格小于行权价格,所以投资者选择行权,即按照K元的价格将手中的标的证券S卖出,获得K元现金;而持有的标的证券S,正好用于行权交割,卖出标的证券,所以投资者最终仍然持有现金K元。
因此,当到期标的证券价格S小于K元时,组合一等于组合二,都是持有现金K元。
(严谨地分析还有第三种情况,到期股价正好等于K元,此时投资者无论是否行权都一样,要么持有K元现金,要么持有价值K元的标的证券S,同样是组合一等于组合二)
综上所述,到期无论什么情况,组合一总是等于组合二。那么根据无套利理论来说,此刻组合一也应该等于组合二,如果不等,必然可以此刻进行买入价值较低组合,卖出价值较高组合,进行无风险套利,最终将套利空间填平,使得组合一等于组合二。因此,平价公式成立。
三、平价公式的理论意义有哪些
(一)初学的投资者通常无法理解期权价格与哪些因素有关,或者关系如何。但是通过上述平价公式,就比较清晰了。
举个例子,其他因素保持不变,如果标的价格S上涨,会导致等式右边(P+S)变大,为了保持等式成立,所以P要减小,或者C增加,所以可以得出认购期权C与标的证券价格正相关,认沽期权P与标的证券价格S负相关;
再比如,其他因素保持不变,行权价格K变大,导致等式左边(C+Ke-rT)变大,为了保持等式成立,所以P要变大,或者C要变小,所以可以得出认购期权C与行权价格负相关,认沽期权P与行权价格正相关。
(二)帮助投资者理解希腊字母的关系
1.Delta
我们知道Delta描述的是标的证券价格变动对期权价格变动影响,用数学含义解释,就是期权价格关于标的证券价格的一阶导数,如果我们公式两边同时求S的一阶导数,我们可以得到c/s=p/s+1,即认购期权的Delta=认沽期权的Delta+1,我们在行情软件中查询结果也是符合这个公式的。
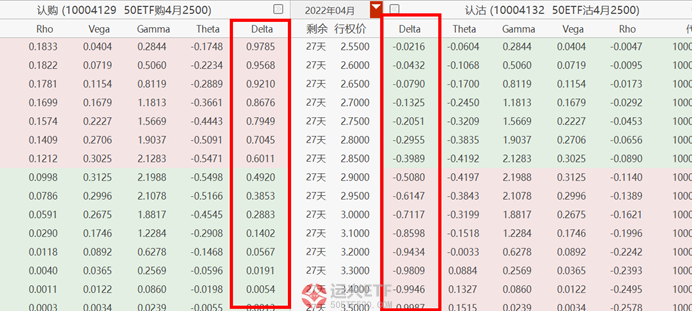
2.Gamma
Gamma描述的是标的证券价格变动对Delta变动的影响,用数学含义解释,就是Delta关于标的证券价格的一阶导数,也是期权价格关于标的证券价格的二阶导数,因此可以得出认购期权的Gamma=认沽期权的Gamma。从行情软件中查询结果,也同样符合这个公式。
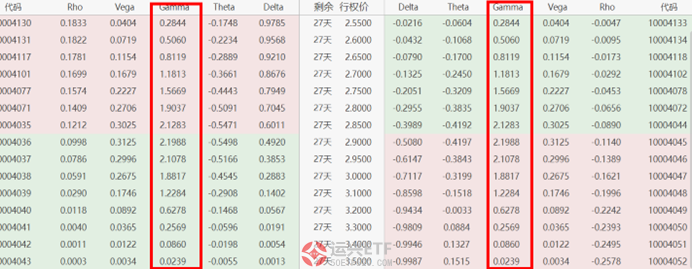
3.Vega与Theta
同样的方法,公式两边分别求关于波动率和时间的导数,可得:
认购的Vega=认沽的Vega
认购的Theta+rKe-r(T-t)=认沽的Theta
而行情软件中同样可以验证这两个特征
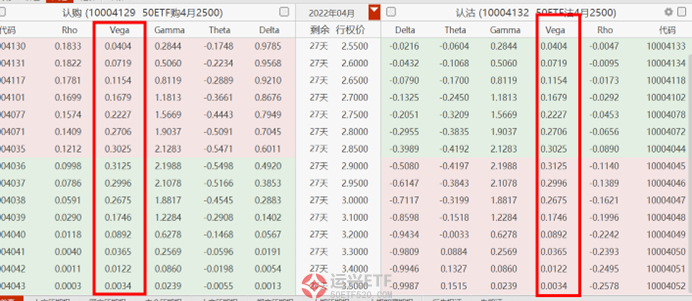
四、平价公式的应用
(一)用于合成各种策略
平价公式等式左右两边可以移动,组合成不同策略,或者产品替代。通过以下几个例子进行说明:
例1:C=P+S-Ke-r(T-t)
从这个公式中我们可以看到,一个认购期权可以用一个认沽期权、一个标的证券和贷入无风险资产进行合成。
例2:S=C-P+Ke-r(T-t)
一个标的证券可以用买认购、一个卖认沽和一个无风险资产组合进行合成。
例3:Ke-r(T-t)=P+S-C
一个无风险利率投资,可以用买认沽、卖认购和买标的证券进行合成。
例4:S-C=Ke-r(T-t)-P
持有标的证券并卖出认购(备兑策略)也等同于卖一个认沽并投资无风险利率资产。
(二)发现套利机会:
实际交易中,如果认购认沽期权价格定价出现异常,可能会出现套利机会,如果套利的收益大于所需的交易成本,那么理论上就有套利的交易空间。
上文中提到S=C-P+Ke-r(T-t),即标的证券S可以用C-P+Ke-r(T-t)组合进行替代,如果S和组合出现不等,就可以买入低估的资产,卖出高估的资产,进行套利交易。案例如下:
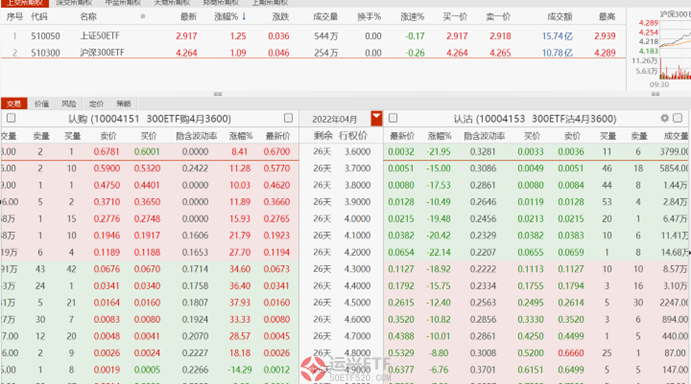
上图是300ETF期权某日行情,我们可以统计出以下数据:
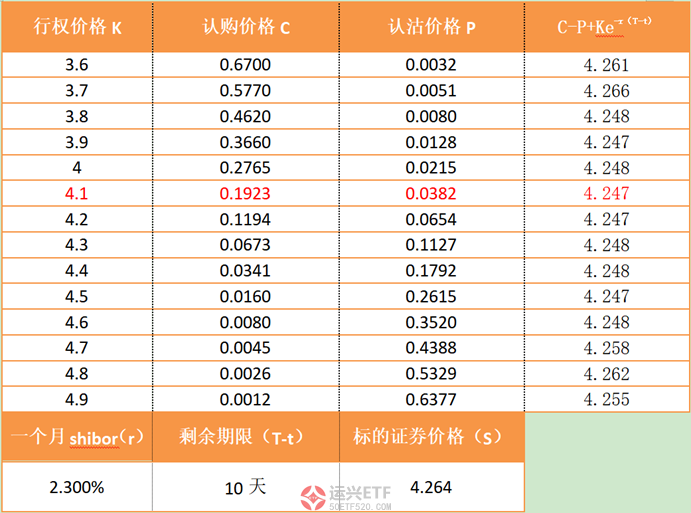
套利方式:以行权价4100合约为例,S(4.264)大于C-P+Ke-r(T-t)的组合(4.247),所以我们可以做空标的证券S,买入组合,具体操作如下所示:
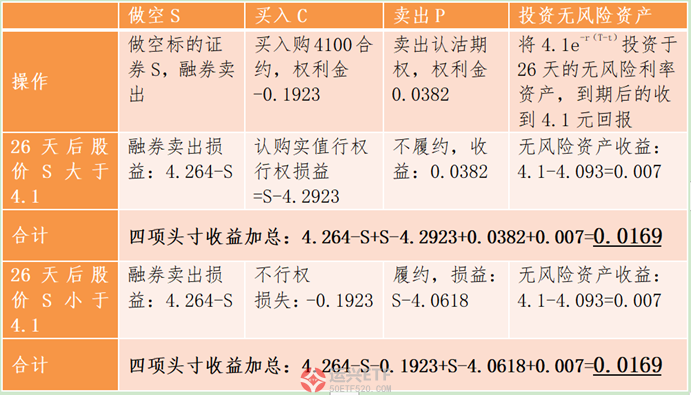
上表可知,26天到期后无论股价大于4.1还是小于4.1,投资者都能获得0.0169元收益。如果该收益高于所有投资成本(包含佣金和利息等),则投资者便可以进行套利交易。
当然,实际投资中还需要考虑下单速度,交易连续性,行权交割时效性等实际问题,这些问题会影响套利交易效率。市场上也有一些交易软件会自动发现套利机会,辅助投资者进行套利交易。
